In our last article, we talked about why it was important to concentrate efforts in the right direction.
That might sound philosophical, but no… it was mathematical. The directions we are referring to are directions in the sense of linear algebra, i.e. the basis vectors of the space used for gravity field modeling. We illustrated how, if given a chosen dimension, we could improve the gravity solution by astutely choosing a set of basis vectors and the subspace generated by those vectors. We would then focus our efforts to search a solution inside this subspace.
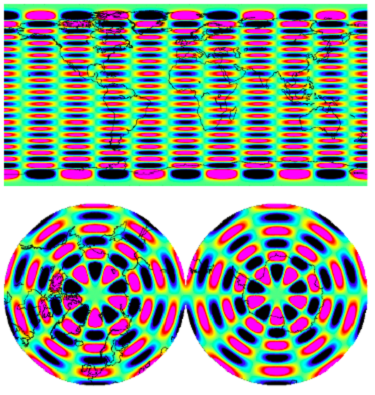
The first subspace is generated by the spherical harmonic functions up to degree and order 50. These are the first 2601 vectors of the canonical basis. The second subspace (the astute one) is made of the first 2601 eigenvectors of the gravity normal matrix.
We saw that our solution in the first subspace would be this:
While the solution in the second subspace would be this: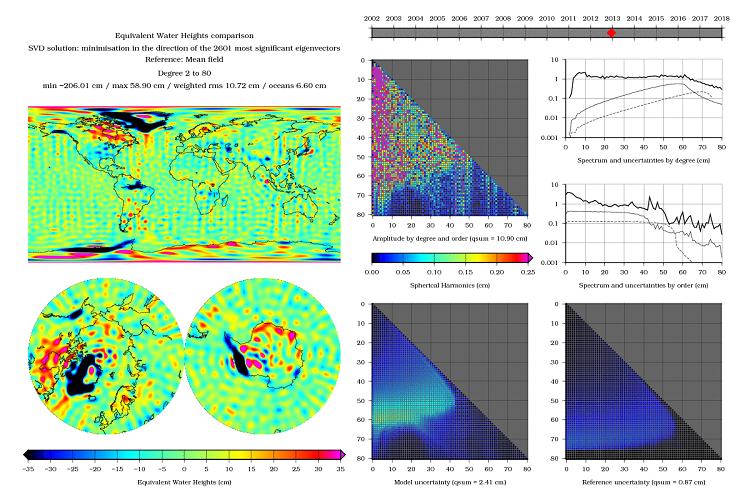
Although the two subspaces are of the same size, the nature of the result is quite different. Indeed, we can get rid of the stripes without any post-inversion filtering, which is very appealing.
In our last essay, we concluded that directions were important. What we didn’t show, however, is what those actual directions « looked like ». This is very important, because it makes clear how we could eliminate the striping.
These are the looks of some standard basis vectors. In our first case, these are the spherical harmonic functions up to degree and order 50.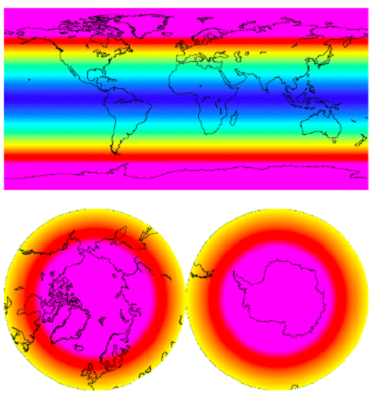
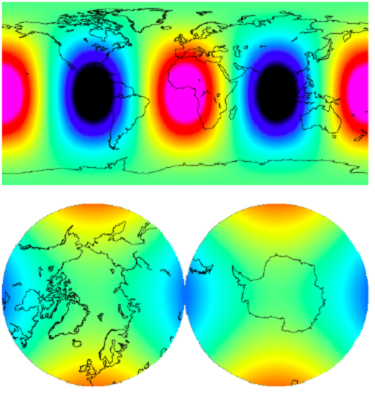
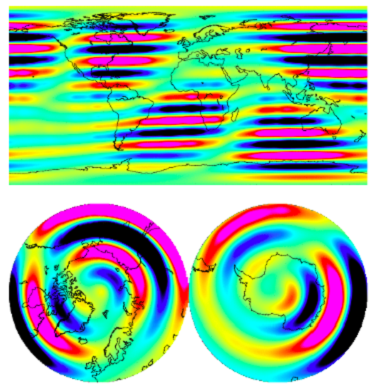
These are the looks of some alternative basis vectors (the eigenvectors).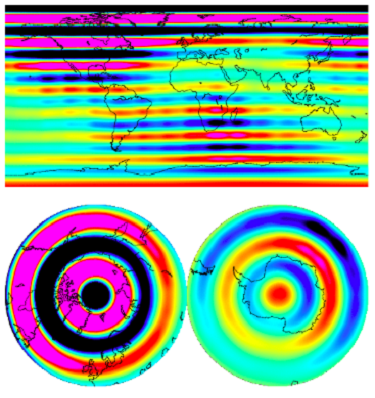

Since we wanted the two subspaces to have the same dimension, we had to discard some directions. i.e. leave aside some eigenvectors of the normal matrix. We kept the ones with higher eigenvalues, and discarded the other ones. The reason for this will be explained in a future article (On the importance of concentrating efforts on the right direction, part 3).
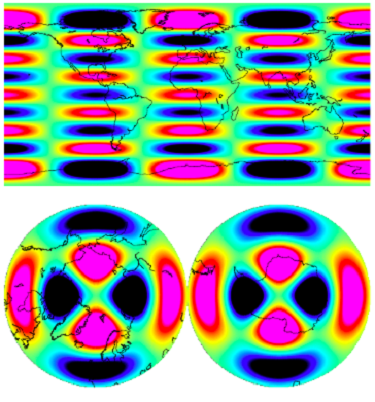
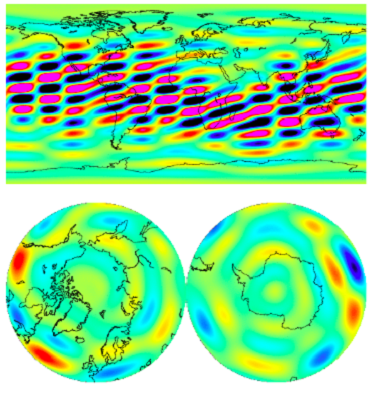
Let’s have a look at the eigenvectors we discarded (the ones with the lower eigenvalues). They look like this: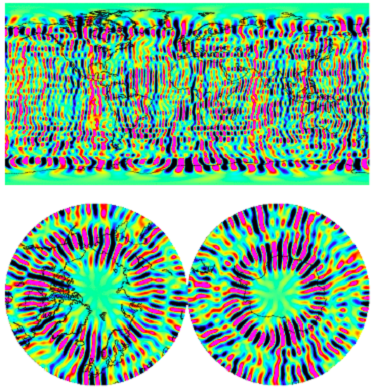
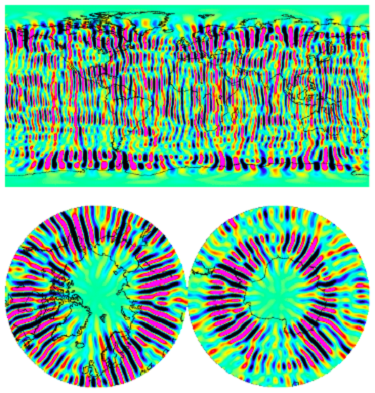
That means that the vectors responsible for the stripes are clearly the ones associated with lower eigenvalues. Discarding them from our gravity subspace guarantees that they will not pollute our solution. This explains how we could obtain the results presented at the start.
Of course, this technique doesn’t guarantee that we are not also removing some part of the signal with this method. But any post-inversion filtering does it for certain. Therefore, it is at least worth studying and comparing the results provided by the two techniques. Since the EGSIEM combined normal equations are now available, we will be able to proceed to this comparison in the future months, and, as usual, you’ll be the first to know the results.
(to be continued…)
